Improving teacher prep in mathematics
UD’s Mathematics Education Program Explores How to Strengthen Teacher Preparation Curriculum
Setting Goals | Research findings | Implications | References
Over the past five years, public conversations around teacher preparation programs have increased as media outlets, politicians, and parents have questioned the value of teacher education.
“There are many alternative programs that compete with traditional teacher preparation programs, like Teach for America,” explained Dawn Berk, assistant professor, UD’s Department of Mathematical Sciences and the School of Education. These programs “stem from the idea that to be a good teacher, you just need to have really strong content knowledge.”
Researchers at UD, however, disagree with that assumption. With continual support from the National Science Foundation (NSF) over the past 15 years, faculty and doctoral students in mathematics education have been working steadily to determine, measure, and improve the value of the teacher preparation program.
Deepening pre-service teachers’ content knowledge and improving instruction
Beginning in 2000, the research group focused on three content courses and one methods course within the mathematics portion of the School of Education’s Elementary Teacher Education (ETE) program. Researchers Berk, Brad Glass, Laura Glass, James Hiebert, Amanda Jansen, and Ann Morris worked to achieve four goals:
- commit to a set of stable, carefully chosen, and realistic learning goals for pre-service teachers,
- develop a consistent, research-based instructional approach that models the approach pre-service teachers should use in the classroom,
- make data-based improvements to the courses and,
- create detailed lesson plans for the next semester’s instructors.
During the first grant period from 2000-2010, the research group identified a limited set of topics for each of the three content courses based on the difficulty level for children.
“We made some hard decisions about which topics we thought were most important,” said Hiebert, Robert J. Barkley Professor in the School of Education. “We made those decisions based on the largest obstacles for elementary school students. When students get to fractions, for example, they struggle and lose interest in math. When these students start falling behind in elementary school, they almost never catch up. Instead, they fall further behind, which eliminates huge categories of careers and life skills.”
The research group also committed to offering UD’s ETE students a particular kind of deep content knowledge that best serves teachers and modeled the instructional approaches that they hoped their students would practice in their own classrooms.
By the end of the first grant period, the research group collected clear evidence that the courses gradually improved over time and that later cohorts were learning mathematics more deeply than earlier groups. The researchers then asked whether this knowledge would lead to more effective teaching in the classroom.
Effectively teaching content in the classroom
To pursue this question, Berk, principal investigator, and co-principal investigators Hiebert and Alfinio Flores (Hollowell Professor of Mathematics Education in the Department of Mathematical Sciences), received a second NSF grant in 2009 to follow graduates of the ETE program into the field. This NSF REESE grant totaled $1,983,506 and allowed them to follow two cohorts of graduates for four years. Each year, the research team followed between 86 and 151 graduates who had accepted teaching positions in Delaware, Maryland, New Jersey, and Pennsylvania. Those who moved further away to teach, or did not teach during the project, still participated by completing some of the measures of mathematics knowledge for teaching.
Berk, Hiebert, and their research colleagues designed and administered measures to assess the knowledge of their graduates through traditional paper and pencil tasks, video exercises, and live observations. They assessed competencies in three math topics that were emphasized in the program (multiplying whole numbers, subtracting fractions, and dividing fractions) and one math topic that was not addressed at all (finding the mean of a small set of whole numbers).
Their data consistently indicated that the graduates were much better prepared to teach the topics developed in their content courses than they were to teach other topics. The impact of the teacher preparation is especially visible, since these graduates showed that they had better knowledge of these topics even up to seven years after learning them.
“The difference is found in their knowledge-of-mathematics-for-teaching, in their ability to analyze teaching, and in the quality of the lessons plans they create—knowledge, skills, and abilities all of which have been shown to correlate with higher-quality mathematics instruction,” explained Berk.
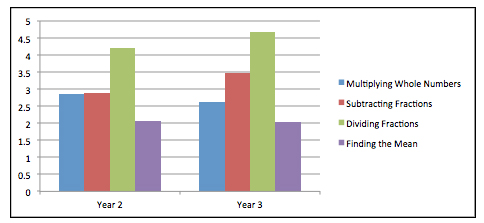
A typical example of the findings comes from a task, analyzed by Morris, Professor in the School of Education, in which graduates were asked to plan a lesson that would introduce each of the four mathematics topics. The lesson plans were scored based on the degree to which graduates attended to the key concepts for each topic when planning the lesson, an indicator of how likely the graduates’ students would develop an understanding of key ideas after they taught the planned lesson. Responses were scored 0-6 for each topic. Results from two and three years beyond graduation are shown in the graph below.
Graph shows graduates’ scores on a task asking them to plan a lesson to introduce each of the four topics to students at an appropriate grade level.
As shown, graduates’ scores were lowest for their lesson plans on Finding the Mean, the topic not taught in the ETE program. Interestingly, scores on Dividing Fractions were the highest, even though this topic is usually considered the most difficult of the four.
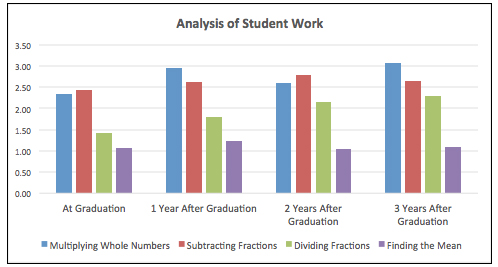
A second example of the findings comes from a task in which Berk and Hiebert asked graduates to analyze school students’ work. For each of the four topics, graduates were shown a student’s solution with a common error or misconception. The graduates were then asked to describe the extent to which the student exhibited conceptual understanding of the topic. Graduates’ responses to this task were scored on whether they noticed the student error, and if so, the extent to which they could uncover the conceptual basis for the error.
Graph shows graduates’ scores on a task asking them to identify and explain common, conceptual errors for specific topics in student work. Graduate responses were scored 0-4, with 0 indicating no identification of the student error.
In each year, graduates’ scores were again lowest for Finding the Mean, the topic not taught in the teacher preparation program.
Given these results, Berk and Hiebert hypothesize a direct relationship between the amount of time spent studying a topic and later teaching performance: the more time that pre-service teachers spend developing deep content knowledge, the more likely they are to retain and apply that knowledge to teaching-related tasks when they become teachers.
Implications and next steps
This work has important implications for teacher preparation programs, which often turn to survey courses as they face increasing pressure to cover all of the many topics listed in the Common Core State Standards. Such survey courses spend only a brief amount of time on each topic, not enough time to enable pre-service teachers to develop deep content knowledge. The initial findings of this research group suggest that such policies should be seriously questioned.
In September 2014, Berk and Hiebert received a new, three-year NSF REAL grant totaling $1,024,667. With this grant, they aim to replicate the previous results and test new hypotheses about specific features of the preparation program as they follow a new cohort of ETE graduates over the next two years.
Listen to this audio podcast on American RadioWorks, with Jim Hiebert discussing his work (25:00)
Relevant References
Morris, A. K., & Hiebert, J. (2015). Openness and measurement: Two principles for improving educational practice and shared instructional products. Mathematics Teacher Educator, 3(2), 130-153.
Hiebert, J. (2013). Transforming teacher preparation to ensure long-term improvement in STEM teaching. Teacher Education and Practice, 26, 830-843.
Bartell, T. G., Webel, C., Bowen, B. & Dyson, D. (2012). Pre-service mathematics teachers’ learning: Recognizing evidence of conceptual understanding. Journal of Mathematics Teacher Education, online first. DOI: 10.1007/s10857-012-9205-4.
Hiebert, J., & Morris, A. K. (2012). Teaching, rather than teachers, as a path toward improving classroom instruction. Journal of Teacher Education, 63, 92-102.
Morris, A. K. (2012). Using “lack of fidelity” to improve teaching. Mathematics Teacher Educator, 1, 71-101.
Morris, A. K., & Hiebert, J. (2011). Creating shared instructional products: An alternative approach to improving teaching. Educational Researcher, 40, 5-14.
Berk, D., & Hiebert, J. (2009). Improving the mathematics preparation of elementary teachers, one lesson at a time. Teachers and Teaching: Theory and Practice, 15, 337-356.
Berk, D., Taber, S. B., Gorowara, C. C., & Poetzl, C. (2009). Developing prospective elementary teachers’ flexibility in the domain of proportional reasoning. Mathematical Thinking and Learning, 11(3), 1–23.
Hiebert, J., & Morris, A. K. (2009). Building a knowledge base for teacher education: An experience in K-8 mathematics teacher preparation. Elementary School Journal, 109, 475-490.
Jansen, A. (2009). Prospective elementary teachers’ motivation to participate in whole-class discussions during mathematics content courses for teachers. Educational Studies in Mathematics, 71(2), 145-160.
Jansen, A., Bartell, T., & Berk, D. (2009). The role of learning goals in building a knowledge base for elementary mathematics teacher education. Elementary School Journal, 109, 525-536.
Jansen, A., & Spitzer, S. M. (2009). Prospective middle school mathematics teachers’ reflective thinking skills: Descriptions of their students’ thinking and interpretations of their teaching. Journal of Mathematics Teacher Education, 12(2), 133-151.
Morris, A. K., & Hiebert, J. (2009). Introduction: Building knowledge bases and improving systems of practice. Elementary School Journal, 109, 429-441.
Morris, A. K., Hiebert, J., & Spitzer, S. M. (2009). Mathematical knowledge for teaching in planning and evaluating instruction: What can preservice teachers learn? Journal for Research in Mathematics Education, 40, 491-529.
Hiebert, J., Morris, A. K., Berk, D., & Jansen, A. (2007). Preparing teachers to learn from teaching. Journal of Teacher Education, 58, 47-61.
Morris, A. K. (2007). Factors affecting pre-service teachers’ evaluations of the validity of students’ mathematical arguments in classroom contexts. Cognition and Instruction, 25 (4), 479-522.
Hiebert, J., Morris, A. K., & Glass, B. (2003). Learning to learn to teach: An “experiment” model for teaching and teacher preparation in mathematics. Journal of Mathematics Teacher Education, 6, 201-222.